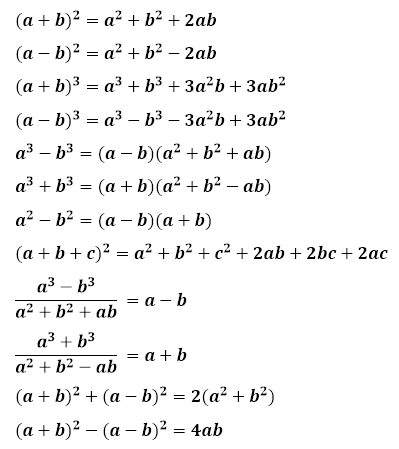Skip to main content

Simplification Questions for competitive exams

Simplification Questions for competitive exams: An introduction

In every competitive exam ,under quantitative aptitude section you can find simplification questions. You can expect simplification and approximation questions in exams like Common Aptitude Test (CAT), MAT, GMAT, IBPS PO,Clerk Exams, CSAT, CLAT, SBI Bank Competitive Exams, ICET, UPSC Competitive Exams, CLAT, SSC CGL, state PSCs, XAT, GRE, Defense service , L.I.C,General insurance and many other competitive examinations. Many candidates take this section very lightly and fail to score well in this section. To avoid minor errors you must thoroughly understand basic maths rules and formulas.Understanding some tricks and shortcuts will improve your calculation speed considerably. Here we have provided basic formulas and shortcuts for solving simplification questions much faster.You can also find three sets of practice questions for simplification below.

BODMAS rule

BODMAS stands for Brackets, Orders, Division, Multiplication, Addition and subtraction. To simplify a mathematical expression you must do brackets first, then division, then multiplication, then addition and subtraction. When all your operations are the same level (for example,division or multiplication, addition or subtraction, powers or roots ), simply work from left to right.

B=Brackets
O=Orders (powers and roots)
D=Division
M=Multiplication
A=Addition
S=Subtraction

Some useful formulas

basic maths equations

Formulas and shortcuts for basic arithmetic operations and simplification

1. Division-shortcuts
In division instead of direct division, use factoring method

Example1:1848/264=(2*3*4*7*11)/(2*3*4*11)=7

Example2:=594/54=(11*9*3*2)/(9*3*2)


2.Multiplication-shortcuts
i)Sum-10 method:Example: 78 and 72. These two numbers, if we add the numbers in the unit's place, the resultant is 10 and the numbers in the ten's place are both the same. In such cases, we can have a simple solution.

Step1: multiply the numbers in the unit's place and write down the result.
(8*2 = 16)

Step2: say, the number in the ten's digit is a, then multiply a*(a+1) and write down the result.
=> (7*(7+1) = 56)

Step3: write the final result: 5616

Example:118*112 follow above steps
8*2 = 16; and 11*(11+1) = 11*12 = 132. And hence the result is: 13216.

In short: ab*ac = (a*(a+1))(b*c)

ii)Base Method:Base numbers, in general, are nothing but multiples of 10. If the given numbers are nearer to base numbers, then you can follow this method to multiply them.

Example: 98*95 =?
Here 98 is ,2 less than the base number 100 and 95 is ,5 less than 100. We can write them like this:
98 -2 


95 -5
The first step will be deducting/subtracting the resultant of the diff between the base number and the given number with the given number in a crossway! That is, you need to subtract 98 and 5 (which is the resultant of difference between the base number and 95) or you can also cross-subtract 95 and 2, the result will be same. This result forms the 1st part of the resultant at the start. The last part of the resultant will be multiplication of the differences from base numbers (i.e., 2 * 5 = 10)
98 -2 

95 -5

 (98 – 5) (-2 * -5)

Hence, the answer will be: 9310

Example: 998*997 =?
998 -2 

997 -3
Observe carefully, in the second part, the multiplication of difference yield in a single digit number, but no. of zeroes in the base number, here 1000, is three. Hence add two zeroes before the result. Therefore, the answer will be:
(998-3) | (-2 * -3) = 995006

What if the numbers we get are like this? I mean, the base is 50 here. We will follow the same procedure as above but a small difference that the resultant in the first part will be halved. And if the base is 200, then the number will be doubled and so on based on the base number.

iii)Multiplication with 5,25,50 etc...
Substitute 5 by 10/2,25 by 100/4 and 50 by 100/2.

Examples: 
1. 5*18=18*10/2=180/2=90 
2. 24*25=24*100/4=2400/4=600
3. 73*50=73*100/2=7300/2=3650

iv)Multiplication with 9, 99,999 etc..

 Examples:
1. 13*9=13*(10-1)=130-13=117 
2. 26*99=26*(100-1)=2600-26=2574
3. 350*999=350*(1000-1)=350000-350=349650
Simplification and approximation practice questions


SBI PO 2017 prelim model question paper pdf download
Labels:

Popular posts from this blog

Square roots and cube roots shortcuts

Here we are sharing some useful shortcut tricks for finding square,cube,square root and cube root which will be helpful in competitive exams. Square-Shortcut Tricks Method1 :Apply Examples: Method2 :Square of a number ending with 5 Suppose X5 is the number. Examples: Method3 :Squres of numbers from 51-59 Add 25 to unit digit and square unit digit and concatenate two results Examples: Method4 :square if you know square of previous number Examples : Method5 :Square of a number if you know square of any other number. Let X and Y be two numbers. You know the square of X then you can deduce square of Y. Example: Choose a nearby number whose square is known to you.Suppose we choose 110 whose square is 12100 Examples: Cubes-Shortcut Apply the formula Examples: Square roots shortcuts (applicable only for perfect squares) Method1: Example1 :Square root of 2704 Step1:Seperate number into group of two from right to left ie 27 04. Step2:Wha...
Read more

Simple Interest and Compound interest shortcut formulas

Here you can find important formulas and time saving shortcut tricks and methods for simple interest and compound interest questions for various competitive exams Simple Interest Interest is said to be simple if it is calculated on the original principal throughout the loan period irrespective of the length of the period of which it is borrowed. Simple interest is given by the formula I= PRT /100 Where P=PRINCIPAL R=RATE OF INTEREST per annum T=TIME PERIOD Principal P=100I/RT Rate of interest R=100I/PT Time period T=100I/PR If principal doubles in T years,then R=100/T If principal triples in T years ,then R=200/T if principal becomes four times in T years,then R=300/T Compound Interest When money is lent at compound interest the interest is calculated at fixed interval of time i.e,at the end of year, half year,quarterly, or even monthly etc.In such cases amount after first unit of time period becomes the principal for second unit of time period,the amount after...
Read more

Geometric Progression :Important formulas

Geometric Progression Geometric Progression (GP) is a sequence, in which next term in the sequence is obtained by multiplying the previous term by a fixed number, and the fixed number is called the Common Ratio. Example : 5,15,45,135   … is a GP with first term 5 and common difference 3 General form of Geometric Progression A geometric sequence or a progression is one in which the ratio between two consecutive terms is constant. This ratio is known as the common ratio denoted by ‘r’, where r ≠ 0. The   elements of the sequence be denoted by: a, ar, ar 2 , ar 3 , … , ar n-1   common ratio ‘r’= successive term/preceding term =a 2 /a 1  = a 3 /a 2  = = a n /a n-1  Types of Geometric Progression Geometric progression can be classified as           Finite Geometric Progression (Finite GP)           Infinite Geometric Progression (Infinite GP) Finite G.P. is a sequence that contains finite t...
Post a Comment
Read more